2018 June 10

伸展树splay

splay是众多平衡二叉搜索树中的一种，其保持平衡的途径也是旋转，最大的区别在于查询操作会引起树结构发生变化，各种操作的均摊复杂度为O(logn)。此外，splay与其他平衡树相比，功能更为强大，支持区间操作，可以进行快速分裂与合并。

splay的基础是BST，通过旋转定义了splay操作，它支持将指定的节点旋转至树根。各种常规操作都建立在splay操作之上。

旋转操作

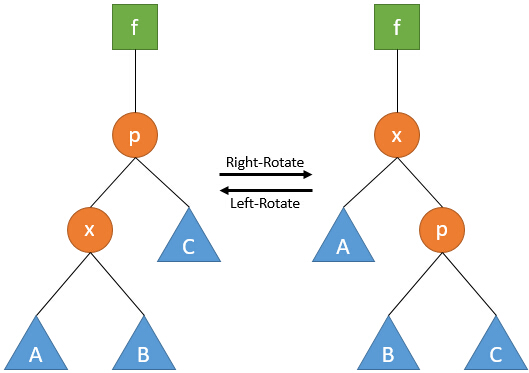
由于节点含有父指针，在旋转时要多维护3个节点的父指针，以及顶端结点的孩子指针。

void RotateL(Node *x) {
    Node *y = x->R; y->P = x->P;
    x->R = y->L; if (x->R) x->R->P = x;
    y->L = x; y->L->P = y;
    Node *p = y->P;
    if (p) {
        if (x == p->L)
            p->L = y;
        else
            p->R = y;
    }
}
void RotateR(Node *x) {
    Node *y = x->L; y->P = x->P;
    x->L = y->R; if (x->L) x->L->P = x;
    y->R = x; y->R->P = y;
    Node *p = y->P;
    if (p) {
        if (x == p->L)
            p->L = y;
        else
            p->R = y;
    }
}

splay操作

根据不同的形态，总共有6种情况需要处理，如果合并镜像操作，有3种情况。

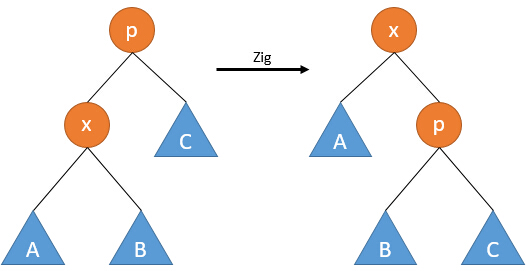
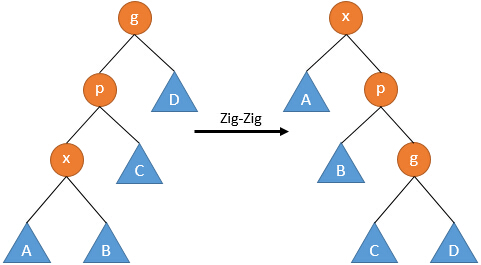
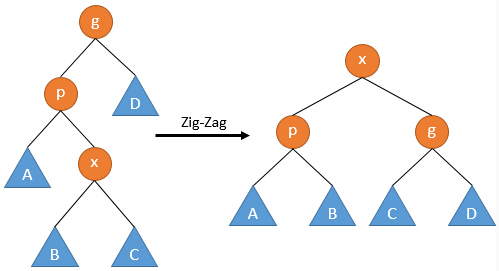
以下接口将节点x旋转为y的子节点。特别的，当y为空指针时，表示将x旋至根。

void Splay(Node *x, Node *y) {
    if (!x) return;
    while (x->P != y) {
        Node *p = x->P;
        if (p->P == y) {
            x == p->L ? RotateR(p) : RotateL(p);
        } else {
            Node *g = p->P;
            if (x == p->L && p == g->L)
                RotateR(g), RotateR(p);
            else if (x == p->R && p == g->R)
                RotateL(g), RotateL(p);
            else if (x == p->L && p == g->R)
                RotateR(p), RotateL(g);
            else
                RotateL(p), RotateR(g);
        }
    }
}

查找节点

Node* SplayFind(Node *&x, int key) {
    Node *t = Find(x, key);
    if (!t) return t;
    Splay(t, nullptr);
    return x = t;
}

插入节点

Node* SplayInsert(Node *&x, int key) {
    Node *t = Insert(x, nullptr, key);
    Splay(t, nullptr);
    return x = t;
}

删除节点

删除节点时，先将待删除节点旋至根，再调BST的接口删除。

Node* SplayDelete(Node *&x, int key) {
    Node *t = SplayFind(x, key);
    if (!t) return t;
    return Delete(x, key);
}

分裂与合并

假设要将树分成左右两部分，左边部分最大值不超过k，右边部分最小值大于k，那么可以先找到键小于等于k的最大节点，将其旋至根，此时该节点的右子树即为右边部分，剩下的为左边部分。

假设要合并两棵树，分别记为L和R，其中L的最大值小于R中的最小值，那么先将L中的最大节点旋至根，此时根肯定没有右子节点，将R作为L树根的右子节点即可。

区间操作

假定要对区间[a,b]做某种操作，记树中键小于a的最大节点为A，键大于b的最小节点为B，将A旋至根，再将B旋至A的子节点，那么键值在区间[a,b]内的所有节点均位于B的左子树中。

Table of Contents