diffie-hellman密钥交换
密钥配送问题
在使用对称密码时,肯定会遇到密钥配送问题。例如,A最近认识了B,现在想给B发消息,但又不想让别人知道消息内容,因此用对称密码对消息做了加密。但B收到密文后无法解密,因为他不知道密钥是什么,而如果A将密钥与密文一起发的话,虽然B可以解密,但窃听者E有了密钥和密文也能知道消息内容。
解决密钥配送问题常用的方法有以下几种:
- 事先约定密钥
- 通过密钥分配中心来解决
- 通过Diffie-Hellman密钥交换来解决
- 通过公钥密码来解决
下面介始Diffie-Hellman密钥交换的方法。
Diffie-Hellman密钥交换
虽然该方法名为密钥交换,但实际上双方并没有真正交换密钥,而是通过计算生成出了一个相同的密钥,因此这种方法也称为Diffie-Hellman密钥协商。
假设现在Alice与Bob需要共享一个对称密码的密钥,此时Eve正在双方之间的通信线路上窃听,Alice和Bob采用Diffie-Hellman密钥交换方法生成共享密钥,步骤如下:
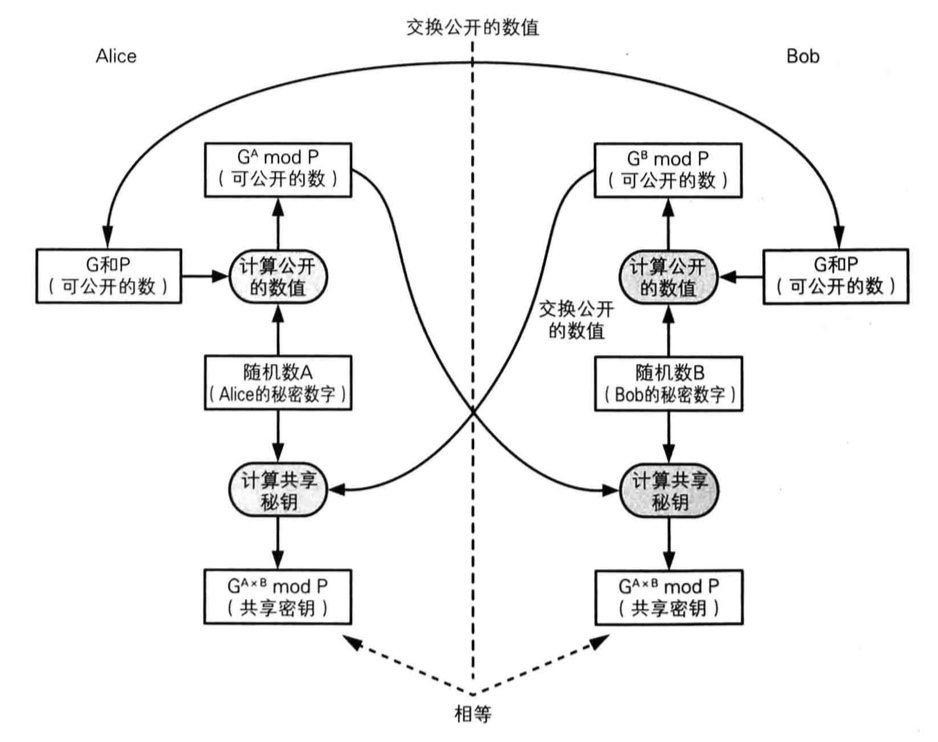
- Alice向Bob发送两个质数P和G
其中P是一个非常大的质数,而G是一个和P相关的数(原根),称为生成元,它可以是一个较小的数字。P和G不需要保密,另外,这两个质数也可以由Bob来生成。
- Alice与Bob各自生成一个随机数
记Alice生成的随机数为A,Bob生成的随机数为B,这两个数字只有生成的人才知道,其他人不知道。
- 交换模P意义下的幂
Alice根据自己生成的随机数A,计算出:X = G ^ A mod P,并把X告知Bob。
同样,Bob计算出:Y = G ^ B mod P,并把Y告知Alice。
- 计算共享密钥
Alice收到Bob发来的Y,计算出共享密钥。
K = Y ^ A mod P = (G ^ B mod P) ^ A mod P = (G ^ B) ^ A mod P = G ^ (A * B) mod P
Bob收到Alice发来的X,计算出共享密钥。
K = X ^ B mod P = (G ^ A mod P) ^ B mod P = (G ^ A) ^ B mod P = G ^ (A * B) mod P
可见,Alice与Bob计算出来的共享密钥是一致的。那么窃听者Eve能算出来吗?
在上述密钥交换过程中,出现在网络上的数字有G,P,X以及Y,仅根据这4个数字是很难求出A和B的,这是个有限群的离散对数问题,而有限群的离散对数问题的复杂度正是支撑Diffie-Hellman密钥交换算法的基础。