最长回文子串之manacher

问题描述

给出一个字符串，求出其最长回文子串。

解决方法

最直接的方法是枚举各个字符作为回文中心，向两边扩展至最大长度，时间复杂度为O(n^2)，注意奇回文与偶回文要分开处理。

另一种做法是按先乘与后乘两种方式预处理出各个位置的哈希值，再二分答案，时间复杂度为O(nlogn)。

下面介绍的manacher算法可在线性时间内求出解。

由于回文分为奇回文和偶回文，为避免分类讨论，在字符间插入一个未在字符串中出现过的字符，全部转成奇回文。为避免越界，在最前端再插一个未出现过字符。例如，s=abbahop，转换后s1=##a#b#b#a#h#o#p#。

定义辅助数组p, p[i]表示以s1[i]为中心的最大回文半径，易见，p[i]-1正好是原字符串中最长回文串的长度。

manacher算法之所以快，是在求p数组时做了优化，避免了很多重复计算。设mx代表以s1[id]为中心的最长回文最右边界，即mx=id+p[id]。

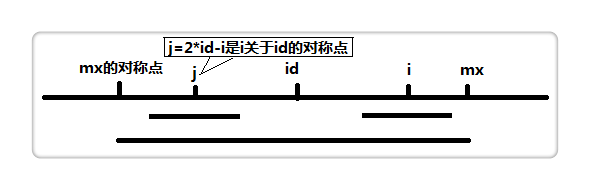
假设现在求p[i]，如果i<mx，那么可直接根据其关于id的对称点j设置p[i]的初值。

#include <bits/stdc++.h>
using namespace std;
char s[100005], s1[200005];
int p[200005], l, ans, mx, id;
int main() {
    scanf("%s", s);
    s1[l++] = '#'; s1[l++] = '#';
    for (int i = 0; s[i]; i++) {
        s1[l++] = s[i];
        s1[l++] = '#';
    }
    for (int i = 1; i < l; i++) {
        if (i < mx)
            p[i] = min(p[2*id-i], mx-i);
        else
            p[i] = 1;
        while (s1[i-p[i]] == s1[i+p[i]]) p[i]++;
        if (mx < i+p[i]) {
            id = i;
            mx = i+p[i];
        }
        ans = max(ans, p[i]-1);
    }
    printf("%d\n", ans);
    return 0;
}