rsa加解密原理
RSA是目前使用最为广泛的公钥密码算法,公钥加密也称为非对称加密,与对称加密的最大区别在于加密与解密使用不同的密钥。
RSA加解密过程
在RSA中,明文、密文和密钥都是数字,假设公钥用二元组(E,N)来表示,私钥用(D,N)来表示,其中E、D、N都是数字,那么加解密过程可表示如下:
密文 = 明文 ^ E mod N (加密)
明文 = 密文 ^ D mod N (解密)
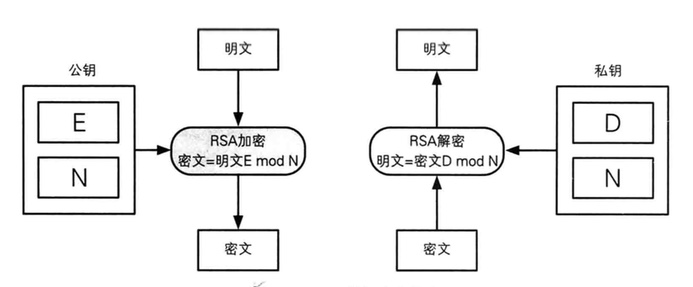
可见,在RSA中,不论加密还是解密,都可归结为求x的y次幂对m取余问题。
生成密钥对
生成RSA密钥可分成以下4步:
- 求N
- 求L(L仅在生成密钥对的过程中使用)
- 求E
- 求D
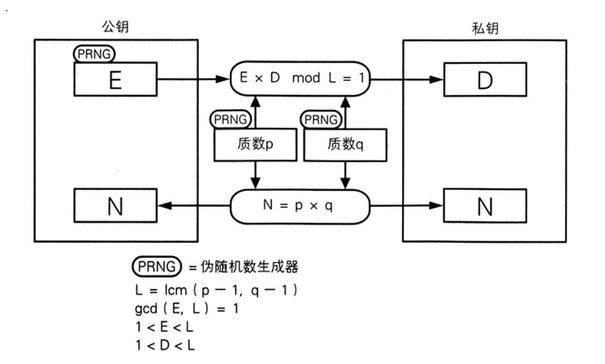
计算N
首先准备两个很大的质数p和q,那么N = p * q。
求L
L = lcm(p-1, q-1)
由于存在恒等式gcd(a,b) * lcm(a,b) = a * b,求lcm可转换为求gcd,而求gcd可通过欧几里德算法在对数时间内算出。
求E
E是一个比1大、比L小的数,且满足E与L互质,即有:gcd(E,L)=1, 1 < E < L。gcd(E,L)=1是为了保证后面要求的数字D一定存在。
可不断地生成[2,L-1]之间的随机数作为E的候选数,检查是否满足条件,直到找出符合要求的E为止。
至此,E和N都已求出,那么公钥(E,N)也就得到了。
求D
数D是由数E计算得到的,D、E和L之间满足关系:E * D mod L = 1, 1 < D < L。
只要D满足上述条件,那么通过E与N加密的内容,就可通过D和N进行解密。
求D也可采用类似求E的方法,不断产生随机数去试,直到找出满足条件的D为止,这样私钥(D,N)也准备好了。
计算示例
生成密钥对
为方面说明,这里用较小的数计算。先准备两个质数,例如,p=17, q=19,那么N=17*19=323,L=lcd(16,18)=144。
满足gcd(E,L)=1的数很多,例如5,7,11,13,25等,这里取E=5。
满足E*D mod L = 1的数也很多,这里取D=29。
到这里,公私钥都有了,公钥为(5,323),私钥为(29,323),公钥可任意公开,私钥则保密。
数据加解密
明文必须是小于N的数,因为加密运算中要求mod N。假设明文是123,用公钥(5,323)对其加密:
密文 = 明文 ^ E mod N = 123 ^ 5 mod 323 = 225
再用私钥(29,323)对密文225进行解密:
明文= 密文 ^ D mod N = 225 ^ 29 mod 323 = 123
解出的明文与原始明文一致。